The theoretical principles of inelastic phenomena in solids were formulated for the first time by C. Zener in 1937 – 1938. Virtually at the same time N. N. Davidenkov
formulated the principles of the nonlinear mechanics of materials. Special literature operates with various terms for describing inelastic phenomena in solids, for example, internal friction, physical acoustics, absorption of ultrasound,
static and dynamic hysteresis loops, internal dissipation of energy, and damping of oscillations. In 1990 De Batist and Magalas suggested a generalized concept for the
description of these phenomena known today as mechanical spectroscopy of materials. Mechanical spectroscopy (MS) studies absorption spectra of mechanical energy under the conditions of applied periodic external mechanical field. The
problem is regularly discussed at international and domestic symposiums and conferences. In Russia the study is coordinated by the Ioffe Physicotechnical Institute of the Russian Academy of Sciences, Voronezh State Engineering University, and Tula State University.
Depending on the nature of the perturbing field F, mechanical spectroscopy analyzes the absorbed or emitted energy for various models of the system involving the perturbation source (F ), the physical object (S ) subjected to the action of the perturbing field, and the response (R ) (see Fig. 1). The external perturbing field and the physical object determine the response R, the method of its determination, and the experimental method.
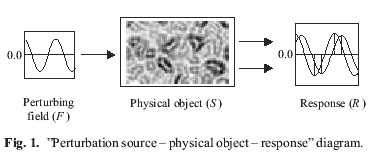
The external perturbing field (F ) causes a new equilibrium state that appears noninstantaneously, which explains why the corresponding relaxation time is not zero. There is a time lag between the response and the perturbation; under periodic loading this gives rise to a hysteresis loop in the coordinates R = f (F ) (at ultimately high frequencies the F and R of the system do not have enough time to interact). Since the hysteresis is accompanied by energy dissipation, the generalized modulus (or “compliance”) of the system can be determined quantitatively from the relation.
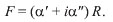
If F is the stress and R is the strain, the response function 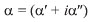 reflects the complex modulus of elasticity M (or rigidity) of the system. If F is the strain and R is the stress, the response function
reflects the complex modulus of elasticity M (or rigidity) of the system. If F is the strain and R is the stress, the response function 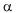 represents the compliance J of the system at M = 1/J.
represents the compliance J of the system at M = 1/J.
The behavior of a physical object under external periodic action is determined by the response function 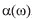 , where the real part
, where the real part 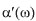 describes the energy stored by the physical object and the imaginary part
describes the energy stored by the physical object and the imaginary part 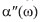 describes the energy dissipated by the physical object; the phase angle
describes the energy dissipated by the physical object; the phase angle 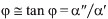 . If the energy losses are low, i.e.,
. If the energy losses are low, i.e., 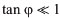 , then
, then 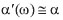 and
and 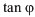 reflects the variation of
reflects the variation of 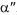 , i.e., the dissipation of energy (mechanical, electrical, dielectric, and other losses). Specialists often use the notion of mechanical quality Q of the system, the reciprocal of which
, i.e., the dissipation of energy (mechanical, electrical, dielectric, and other losses). Specialists often use the notion of mechanical quality Q of the system, the reciprocal of which 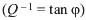 is denoted as the Internal Friction (IF). In a linear approximation (at low absorption of energy) the quantities describing the internal dissipation are related as follows:
is denoted as the Internal Friction (IF). In a linear approximation (at low absorption of energy) the quantities describing the internal dissipation are related as follows:
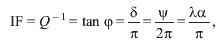
where 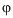 is the phase angle between the stress and the strain,
is the phase angle between the stress and the strain, 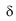 is the logarithmic decrement of the oscillation,
is the logarithmic decrement of the oscillation,  is the relative energy dissipation per oscillation cycle (the damping capacity),
is the relative energy dissipation per oscillation cycle (the damping capacity), 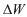 is the dissipated energy, W is the energy of mechanical oscillation of the system,
is the dissipated energy, W is the energy of mechanical oscillation of the system, 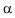 is the coefficient of absorption of ultrasound, and
is the coefficient of absorption of ultrasound, and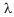 is the wavelength. In general the MS response in a solid body is represented by the elastic M(J ) and inelastic
is the wavelength. In general the MS response in a solid body is represented by the elastic M(J ) and inelastic 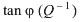 characteristics of mechanical oscillation.
characteristics of mechanical oscillation.
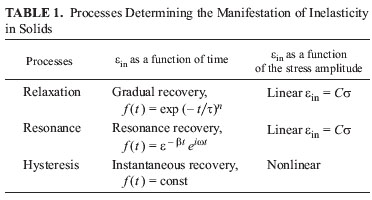

Problems of the theory of inelastic phenomena in metals and alloys were considered in detail and classified in the Russian literature in [1] in 1964. It was shown that in actual solid bodies the stress 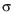 and the strain
and the strain 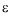 are related through a time dependence and the strain is representable as the sum of two components, i.e.,
are related through a time dependence and the strain is representable as the sum of two components, i.e., 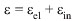 in , where
in , where 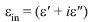 is the inelastic (additional) strain that attains equilibrium with time (quasi-elastic strain). On the whole,
is the inelastic (additional) strain that attains equilibrium with time (quasi-elastic strain). On the whole,  and
and 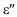 are the components of inelasticity shifted by
are the components of inelasticity shifted by 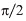 relative to the applied field. They depend on the time, frequency, and temperature; for nonlinear systems they also depend on the value (amplitude) of the stress. The laws regulating the variation of the additional strain with the stress amplitude and time have made it possible to classify the inelastic phenomena in solids (see Table 1).
relative to the applied field. They depend on the time, frequency, and temperature; for nonlinear systems they also depend on the value (amplitude) of the stress. The laws regulating the variation of the additional strain with the stress amplitude and time have made it possible to classify the inelastic phenomena in solids (see Table 1).
References:
1. M. A. Krishtal, Yu. V. Piguzov, and S. A. Golovin, Internal Friction in Metals and Alloys [in Russian], Metallurgizdat, Moscow (1964).
2. S. A. Golovin, METHODS OF MECHANICAL SPECTROSCOPY IN PHYSICAL METALLURGY, Metal Science and Heat Treatment Vol. 44, Nos.5–6, 2002